Next: Bibliography Up: True Path Rule hierarchical Previous: Classification of specific FunCat
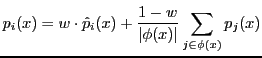
Fig. 7 and 8 show the hierarchical precision, recall and F-measure as functions of the parameter ![]() .
For small values of
.
For small values of ![]() (
(![]() can vary from 0 to 1) the weight of the decision of the parent local predictor is small, and the ensemble decision
depends mainly by the positive predictions of the offsprings nodes(classifiers): in this case we obtain a higher hierarchical recall for the TPR-w ensemble.
On the contrary higher values of
can vary from 0 to 1) the weight of the decision of the parent local predictor is small, and the ensemble decision
depends mainly by the positive predictions of the offsprings nodes(classifiers): in this case we obtain a higher hierarchical recall for the TPR-w ensemble.
On the contrary higher values of ![]() correspond to a higher weight of the ``parent'' local predictor, with a resulting higher precision.
The opposite trends of precision and recall are quite clear in all graphs of Fig. 7. The best F-score is in ``middle'' values
of the parameter parent-weight: in practice in most of the analyzed data sets the best F-measure is achieved for
correspond to a higher weight of the ``parent'' local predictor, with a resulting higher precision.
The opposite trends of precision and recall are quite clear in all graphs of Fig. 7. The best F-score is in ``middle'' values
of the parameter parent-weight: in practice in most of the analyzed data sets the best F-measure is achieved for ![]() between
between ![]() and
and ![]() , but if we need higher
recall rates (at the expense of the precision) we can choose lower
, but if we need higher
recall rates (at the expense of the precision) we can choose lower ![]() values, and higher values of
values, and higher values of ![]() are needed if precision is our first aim.
are needed if precision is our first aim.
|
|