

Next: Clusterv tutorial
Up: The clusterv R package:
Previous: Overview of the clusterv
Background on random projections in euclidean spaces
Dimensionality reduction may be obtained by mapping points from a high to a low-dimensional space, approximately preserving some
characteristics, i.e. the distances between points.
In this context randomized embeddings with low distortion represent a key concept.
Randomized embeddings have been successfully applied both to combinatorial optimization and data compression [12].
A randomized embedding between 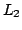 normed metric spaces with distortion
normed metric spaces with distortion 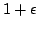 , with
, with 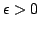 and failure probability
and failure probability 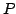 is a distribution probability over mappings
is a distribution probability over mappings
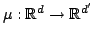 ,
such that for every pair
,
such that for every pair
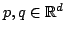 , the following property holds with probability
, the following property holds with probability 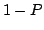 :
:
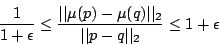 |
(1) |
The main result on randomized embedding is due to Johnson and Lindenstrauss [13], who proved the existence
of a randomized embedding
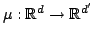 with distortion
with distortion 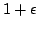 and
failure probability
and
failure probability
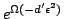 , for every
, for every
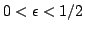 .
As a consequence, for a fixed data set
.
As a consequence, for a fixed data set
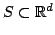 , with
, with 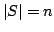 , by union bound, for all
, by union bound, for all 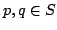 , it holds:
, it holds:
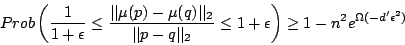 |
(2) |
Hence, by choosing 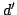 such that
such that
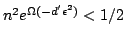 , it is proved the following:
, it is proved the following:
Johnson-Lindenstrauss (JL) lemma: Given a set  with
with 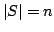 there exists a
there exists a 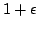 -distortion embedding into
-distortion embedding into
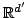 with
with
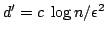 , where
, where 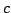 is a suitable constant.
is a suitable constant.
The embedding exhibited in [13] consists in random projections from
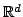 into
into
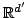 , represented
by matrices
, represented
by matrices 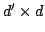 with random orthonormal vectors.
Similar results may be obtained by using simpler embeddings, represented through random
with random orthonormal vectors.
Similar results may be obtained by using simpler embeddings, represented through random 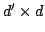 matrices
matrices
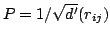 , where
, where 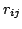 are random variables such that:
are random variables such that:
For sake of simplicity, we call random projections even this kind of embeddings.
We may build random matrices 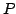 in different ways to obtain random projections obeying the Johnson-Lindenstrauss
lemma:
in different ways to obtain random projections obeying the Johnson-Lindenstrauss
lemma:
- The Plus-Minus-One (PMO) projection:
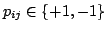 ,
, 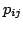 randomly chosen such that:
randomly chosen such that:
- The Achlioptas projection [1]:
- Generalized Achlioptas projection:
with
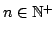 .
.
- A Normal projection:
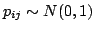 .
.
- Other projections such that:
A particular case of randomized map is represented by Random Subspace (RS) projections [11].
Indeed these projections do not satisfy the JL lemma and may induce large distortions into the projected data.
They are represented by 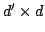 matrices
matrices
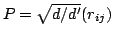 , where
, where 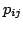 are uniformly chosen with entries in
are uniformly chosen with entries in 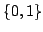 , and with exactly one
, and with exactly one 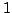 per row and at most one
per row and at most one 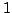 per column.
It is worth noting that, in this case,
the "compressed" data set
per column.
It is worth noting that, in this case,
the "compressed" data set
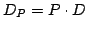 can be quickly computed in time
can be quickly computed in time
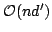 , independently from
, independently from 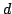 .
Unfortunately, it easy to see that in this case
.
Unfortunately, it easy to see that in this case
![$E[p_{ij}] \neq 0$](img42.gif) and
and
![$Var[p_{ij}] \neq 1$](img43.gif) and hence
RS does not satisfy the JL lemma.
and hence
RS does not satisfy the JL lemma.


Next: Clusterv tutorial
Up: The clusterv R package:
Previous: Overview of the clusterv
Giorgio
2006-08-16
![]() normed metric spaces with distortion
normed metric spaces with distortion ![]() , with
, with ![]() and failure probability
and failure probability ![]() is a distribution probability over mappings
is a distribution probability over mappings
![]() ,
such that for every pair
,
such that for every pair
![]() , the following property holds with probability
, the following property holds with probability ![]() :
:
![]() into
into
![]() , represented
by matrices
, represented
by matrices ![]() with random orthonormal vectors.
Similar results may be obtained by using simpler embeddings, represented through random
with random orthonormal vectors.
Similar results may be obtained by using simpler embeddings, represented through random ![]() matrices
matrices
![]() , where
, where ![]() are random variables such that:
are random variables such that:
![]() in different ways to obtain random projections obeying the Johnson-Lindenstrauss
lemma:
in different ways to obtain random projections obeying the Johnson-Lindenstrauss
lemma:
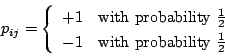
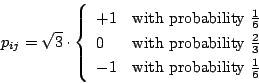
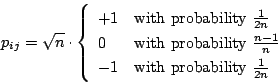
![\begin{eqnarray*}
E[p_{ij}] & = & 0 \\
Var[p_{ij}] & = & 1 \\
\end{eqnarray*}](img35.gif)
![]() matrices
matrices
![]() , where
, where ![]() are uniformly chosen with entries in
are uniformly chosen with entries in ![]() , and with exactly one
, and with exactly one ![]() per row and at most one
per row and at most one ![]() per column.
It is worth noting that, in this case,
the "compressed" data set
per column.
It is worth noting that, in this case,
the "compressed" data set
![]() can be quickly computed in time
can be quickly computed in time
![]() , independently from
, independently from ![]() .
Unfortunately, it easy to see that in this case
.
Unfortunately, it easy to see that in this case
![]() and
and
![]() and hence
RS does not satisfy the JL lemma.
and hence
RS does not satisfy the JL lemma.