

Next: Introduction to the functionalities
Up: Background on stability based
Previous: Stability indices
Statistical tests to assess the significance of clustering solutions
Consider a set of k-clusterings
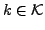 , where
, where 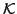 is a set of numbers of clusters and the
corresponding set of integrals computed according to eq. 2. Then we obtain a set of values
is a set of numbers of clusters and the
corresponding set of integrals computed according to eq. 2. Then we obtain a set of values
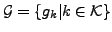 .
We can sort G obtaining
.
We can sort G obtaining
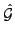 with values
with values 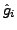 in ascending order.
For each k-clustering we consider two groups of pairwise clustering similarities values separated by a threshold
in ascending order.
For each k-clustering we consider two groups of pairwise clustering similarities values separated by a threshold 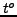 (a reasonable threshold could be
(a reasonable threshold could be 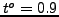 .).
Thus we may obtain:
.).
Thus we may obtain:
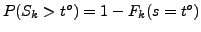 ,
where
,
where 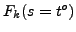 is computed according to eq. 1. If
is computed according to eq. 1. If 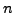 represents the number of trials for estimating the
value of
represents the number of trials for estimating the
value of 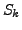 then
then
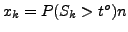 is the number of times for which the similarity values are larger than
is the number of times for which the similarity values are larger than 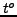 .
The
.
The 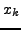 may be interpreted as the successes from
may be interpreted as the successes from 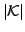 binomial populations with
parameters
binomial populations with
parameters 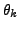 . If the number of trials
. If the number of trials 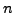 is sufficiently large, and setting
is sufficiently large, and setting 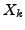 as a random variable that counts
how many times
as a random variable that counts
how many times 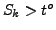 , we have that the following random variable, for sufficiently large values of
, we have that the following random variable, for sufficiently large values of 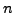 is distributed according
to a normal distribution:
is distributed according
to a normal distribution:
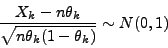 |
(5) |
A sum of i.i.d. squared normal variables is distributed according to a 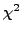 distribution:
distribution:
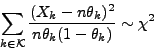 |
(6) |
Considering the null hypothesis 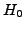 : all the
: all the 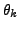 are equal to
are equal to 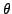 , where the unknown
, where the unknown 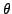 is
estimated through its pooled estimate
is
estimated through its pooled estimate
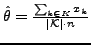 ,
then the null hypothesis may be evaluated against the alternative hypothesis that the
,
then the null hypothesis may be evaluated against the alternative hypothesis that the 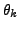 are not all equal
using the statistic
are not all equal
using the statistic
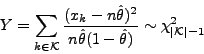 |
(7) |
If
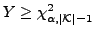 we may reject the null hypothesis at
we may reject the null hypothesis at 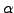 significance level, that
is we may conclude that with probability
significance level, that
is we may conclude that with probability 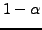 the considered proportions are different, and hence that at least
one k-clustering significantly differ from the others.
Using the above test we start considering all the k-clustering. If a significant
difference is registered according to the statistical test we exclude the last clustering
(according to the sorting of
the considered proportions are different, and hence that at least
one k-clustering significantly differ from the others.
Using the above test we start considering all the k-clustering. If a significant
difference is registered according to the statistical test we exclude the last clustering
(according to the sorting of 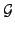 ). This is repeated until no significant difference is detected (or until only 1 clustering is left off): the set of
the remaining (top sorted) k-clusterings represents the set of the estimate stable number of clusters discovered (at
). This is repeated until no significant difference is detected (or until only 1 clustering is left off): the set of
the remaining (top sorted) k-clusterings represents the set of the estimate stable number of clusters discovered (at
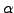 significance level).
significance level).
It is worth noting that the above 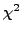 -based procedure be also applied to automatically find the optimal number
of clusters independently of the applied perturbation method.
-based procedure be also applied to automatically find the optimal number
of clusters independently of the applied perturbation method.
Anyway, note that with the previous 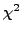 -based statistical test we implicitly assume that some probability distributions are normal.
Using the classical Bernstein inequality [12] we may apply a partially "distribution independent" approach to assess the significance of the discovered clustering.
In this way we can apply a statistical test without any assumption about the distribution of the random variables. For more details see [5],
downloadable from:
-based statistical test we implicitly assume that some probability distributions are normal.
Using the classical Bernstein inequality [12] we may apply a partially "distribution independent" approach to assess the significance of the discovered clustering.
In this way we can apply a statistical test without any assumption about the distribution of the random variables. For more details see [5],
downloadable from:
http://homes.dsi.unimi.it/valenti/papers/bertoni-vale-cisi06.pdf.


Next: Introduction to the functionalities
Up: Background on stability based
Previous: Stability indices
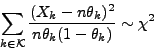
![]() we may reject the null hypothesis at
we may reject the null hypothesis at ![]() significance level, that
is we may conclude that with probability
significance level, that
is we may conclude that with probability ![]() the considered proportions are different, and hence that at least
one k-clustering significantly differ from the others.
Using the above test we start considering all the k-clustering. If a significant
difference is registered according to the statistical test we exclude the last clustering
(according to the sorting of
the considered proportions are different, and hence that at least
one k-clustering significantly differ from the others.
Using the above test we start considering all the k-clustering. If a significant
difference is registered according to the statistical test we exclude the last clustering
(according to the sorting of ![]() ). This is repeated until no significant difference is detected (or until only 1 clustering is left off): the set of
the remaining (top sorted) k-clusterings represents the set of the estimate stable number of clusters discovered (at
). This is repeated until no significant difference is detected (or until only 1 clustering is left off): the set of
the remaining (top sorted) k-clusterings represents the set of the estimate stable number of clusters discovered (at
![]() significance level).
significance level).
![]() -based procedure be also applied to automatically find the optimal number
of clusters independently of the applied perturbation method.
-based procedure be also applied to automatically find the optimal number
of clusters independently of the applied perturbation method.
![]() -based statistical test we implicitly assume that some probability distributions are normal.
Using the classical Bernstein inequality [12] we may apply a partially "distribution independent" approach to assess the significance of the discovered clustering.
In this way we can apply a statistical test without any assumption about the distribution of the random variables. For more details see [5],
downloadable from:
-based statistical test we implicitly assume that some probability distributions are normal.
Using the classical Bernstein inequality [12] we may apply a partially "distribution independent" approach to assess the significance of the discovered clustering.
In this way we can apply a statistical test without any assumption about the distribution of the random variables. For more details see [5],
downloadable from: